How to calculate home loan EMI?
Taking a loan on EMI is a good option, but do you know how to calculate EMI? It’s not just about a Home loan, it can be any loan EMI.
In this post I will tell you how does the monthly EMI for Home Loan is calculated and how increasing Tenure does not help much after a certain point.

What is EMI?
EMI is an abbreviation of Equated Monthly Installments. The name itself explains what does it exactly means. It’s a monthly installment that a borrower has to pay to the bank or the financial institute from where he has taken the loan.
This EMI depends upon the principle amount of loan and tenure i.e. years for which the loan has been taken.
How to calculate EMI?
EMI can be calculated on the basis of 3 terms, which are as –
- Loan Amount
- Interest Rate
- Loan Period
The formula for calculating EMI is given below.
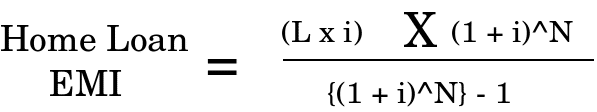
Where,
L = Loan amount
i = Interest Rate (rate per annum divided by 12)
^ = to the power of
N = loan period in months
A lot of people do not know that increasing the tenure only leads to increase in Interest amount payable and nothing else . The decrease in EMI is not proportional to the increase in Loan tenure.
In Housing Finance, Equated Monthly Installments (EMI) refers to the monthly payment towards interest and principal made by a borrower to a lender. Have a look at the example given below to get a clear idea about it.
Example
Assuming a loan of Rs 1 Lakh at 11 percent per annum, repayable in 15 years, the EMI calculation using the formula will be :
[su_table]
| EMI = | (100000 x .00916) x ((1+.00916)^180 ) / ([(1+.00916)^180] – 1) |
| EMI = | 916 X (5.161846 / 4.161846) |
| EMI = | Rs 1,136 |
[/su_table]
Note at i = 11 percent / 12 = .11/12 = .00916
You must have got an idea about calculating EMI. Some people think that increasing the tenure of EMI is a good option because it will help to reduce the EMI.
EMI Calculator:
[CP_CALCULATED_FIELDS id=”9″]
Q. How much benefit we get by increasing the Tenure of the Loan. Considering a Loan of Rs 30 Lacs at 12% interest rate.
Ans: I did a bit of my so-called “mathematical skills” … and found out that EMI is of form
EMI(n) = C1 X C2^n / C2^n-1 , where
C1 = L * i
C2 = 1+i
So the difference in the EMI value for n+1 and n is nothing but
by a bit of calculation I got :
EMI(n) – EMI(n+1) = C1 x (C2^2n – C2^n) / (C2^2n – 1)
and when n becomes very large … and applying limit, we get
Lim C1 x (C2^2n – C2^n) / (C2^2n – 1)
-> Inf=>
Lim C1 / C2^n
n->Infand as C2 > 1 (C2 = 1+i)
=>
Lim C1/C2^n = 0
n->Inf
Or in other words, if we differentiate the EMI formula … we get a constant …
It shows and proves that the difference in EMI value is not very significant compared to the change in tenure and at one stage its almost of no gain to increase the tenure.
To show this argument: I would like to present an example, considering my old question:
Q. How much benefit we get by increasing the Tenure of the Loan. Considering a Loan of Rs 30 Lacs at 10% interest rate.
See the table given below. In this table, i have shown how EMI changes with increasing tenure, and also the difference in your old EMI and new EMI you will have to pay after increasing the tenure.
[su_table]
| Period | New EMI | Difference between old & new EMI |
| 10 | 39645 | |
| 15 | 32238 | 7407 |
| 20 | 28950 | 3288 |
| 25 | 27261 | 1689 |
| 30 | 26327 | 934 |
| 35 | 25790 | 537 |
| 40 | 25474 | 316 |
| 45 | 25286 | 188 |
| 50 | 25173 | 113 |
| 55 | 25104 | 69 |
| 60 | 25063 | 41 |
| 65 | 25038 | 25 |
| 70 | 25023 | 15 |
| 75 | 25014 | 9 |
| 80 | 25008 | 6 |
| 85 | 25005 | 3 |
| 90 | 25003 | 2 |
| 95 | 25001 | 2 |
| 100 | 25001 | 0 |
[/su_table]
From this table you must have realized that after a particular time there is no sense in increasing the tenure because the difference between your old EMI and new EMI will be in some rupees which is negligible.
So it is advisable not to extend your loan tenure to much just to reduce the EMI.
EMI calculators of different banks
Interest rate on loan is different for different banks. So the EMI you will have to pay is also different from bank to bank. In the table given below, I have enlisted some top banks and their EMI calculators link. Click on the links to check the EMI of different banks.
[su_table]
[/su_table]
Tips before taking loan on EMI
- Check the EMI’s of all banks before tanking loan
- Don’t extend your loan tenure just to reduce the EMI
- Negotiate with your agent or loan providing institute when you are planning to take a big amount of loan
- Pay your EMI on time
- Make sure you have a good credit history and you are eligible for home loan before applying.
- Do not expect from a sales person in a bank or the institute from where you are lending money to tech you how to use it. If you are taking a house loan then research for all the related expenses on your own and spend it accordingly.
- And finally, collect all the documents after repaying your loan.
Taking loan is not a bad thing and it doesn’t carry a risk with it, but its only then when you manage it properly. If you have any doubts regarding this information please leave your query in the comment section.
 January 18, 2008
January 18, 2008 
Suggestion on Part payment and Interest Payable
CASE 1
I take a home loan of 300000 lakhs @9.4% for 10 years. Total interest payable by end of 10 years to bank is approx 16 lakhs (calculated online)
CASE 2
I take a home loan of 300000 lakhs @9.4% for 20 years. If I do part payments annually (say 2/3 lakhs every year) along with regular EMI’s ; and repay the loan amount in 10 years ; will my total interest payable to bank be the same as CASE 1 (i.e. 16 lakhs)
Since time taken to repay is 10 years in both cases.
I want to Rental Loan form the Bank. And my lease agreement is for 9 years and my monthly rent is Rs.1,50,000/- which Increase every year 5% .
Request you please guide me how to get add my yearly 5% increase amount with my Original Rent 1,50,000 + 7500 =1,57,500 How to take and add my above amount every year.
Hi Rahul
I am not clear on what is your question. Please repeat it with more clarity
Manish
Dear Manish,
I got a home loan from a co-operative bank. the details are as follows:-
Loan Amount: 15 Lakhs
Tenure: 180 months
Interest Rate : 12 % (Floating rate of interest)
The things is we have been paying the EMI of 18,003 regularly, but some months back the Bank changed the Rate of Interest but did not inform us of the change & we kept on repaying at 12%. The new borrowers are charged an rate of interest of 10.25% currently.
Which we feel is cheated, as the document clearly states that we have got a loan on floating rate of interest, and we should have also been passed on the benefit of rate cute & availed rate of interest of 10.25%.
After we questioned the bank, they were caught a spot of bother.
The bank is giving us an option of closing the current loan account & giving us a fresh loan on the remaining principal amount at 10.25%.
We feel we would end up paying more in such case. They are considering the last unpaid principal amount & this will attract high interest amount as the loan will be a fresh one.
Request your guidance, as how much should be the loan amount (Principal to be paid) if we were to be charged as per floating rate policy (according to RBI rules).
To simplify, giving the actual scenario.
Loan amount = 15 Lakhs.
Rate of Interest = 12%
EMI = 18003 for 180 months.
EMI paid for last 53 months = 18003*53 = 954159
According to bank Principal left to be paid = 12,91,485
Now, they will start a new loan account with this as loan amount & the EMI for this wil be Rs. 16702.
So, we would like to know under normal Floating interest rate account what should be the EMI for the 54th month installment if the tenure remains the same. (i,e. 53 months paid at 12% ROI & next 127 months paid at 10.25%)
Please help.
Hi Rajan
This is very specific query which you should follow up with the concerned authority only. We wont be able to comment on that
Manish
Hi,
i have taken home loan of amt-13,50,000/- from SBI for 15yrs @9.55% …now this month i been paid 6,91,320/- as part disbursment, but bank say my emi is 14,300/- to be start from next month. Here is the doubt unless they paid full amt how they are calculating the emi on total loan value and how the emi comes with a value of 14,300/- i cant understand, please help me if there are some undercover rules for home loan not known to me……..
Note that the EMI is same, but now the tenure will come down .. If you keep the low EMI, then the tenure will be still be same !
Hi Rahul,
I have a home loan of 2500000 for 16 years at 9.75% interest rate. I want to take full benefit of tax exemption of 2 lacs on interest. So just want to know how much should I pay in the year to get the full benefit.
Thanks,
Ashish
That calls for a seperate article ! . I suggest as of now talk to your bank loan lender. They will guide you on this
Hi,
Say, i am going to take a home loan in SBI for 30Lakhs, interest rate 10.0%. Now if i quote
1. for 360 months, the emi will be 26328
2. for 240 months, the emi will be 28951
how much will i save, if i opt for 360 months and pay 60,000 as part payment every year?
thanks
Arun
In that case it would be much less than 240 months !
ya thank you !!!!
Hi Manish,
I have taken a loan from LICHFL amounting 15 lacs out of which they have disbursed around 6 lacs.
This month they sent message of EMI due on 10th July for Rs. 13537. Ideally this amount of EMI is applicable only after 100 % disbursement.
They say you have to options i.e. pay as per disbursement or start the full EMI right from the beginning.
I don’t understand what to do. Please throw some light over this and guide.
Thanks
Hi Rahul
This is very specific query which you should follow up with the concerned authority only. We wont be able to comment on that
Manish
Bank provides 2 options :
1.pay as per disbursement : It means you need to pay interest only for disbursed amount until full amount get disbursed .After full amount disbursed ,Full EMI will start .
2.start the full EMI right from the beginning:
From 1st disbursement onward start paying full EMI .Initially Principle component will be more and interest component will be less in EMI .
If you have money to pay ,it is good to go with 2nd option because less outstanding amount will cause less interest to pay.
loan amount rs.1000000 rate of interest 9.90% tenure of repayment 240 months what amount of monthly emi.
Use this calculator – http://jagoinvestor.dev.diginnovators.site/calculators/html/EMI-Calculator.html
pls let me know the calculation for loan amounting to 150000 at 2.99 as intrest with 36months and 189000 at 2.99 as intrest for 48 months.
loan amount rs.1200000 rate of interest 10.5% tenure of repayment 114 months, after the fourth emi i will do a partial prepayment of Rs.500000 keeping the tenure same what will be the revised emi
Hi badrinath
It’s not so straight forward. Ask bank on this and they shall be able to help you on this
Hi Neil
Your cases is a bit complex and I think we are not the right people to comment on it.
My suggestion would be hire someone who is professional in this area and consult them
Manish
Dear Manish,
I had taken home loan of Rs 21 L from LICHFL for 20 yrs in July 2009. For only about four months the rate was 8.75% and then they increased to 12%, its continued so till now. I paid EMI of 22007. Now I have savings and want to return the loan ASAP. Is it a good strategy if I pay RS 10 Lakhs now and then the rest (My o/s loan is 19,40,000) after another three months from our savings (my, husband and daughter). Some people say it was useful had you paid in small amounts from the beginning. Now its not very useful to pay, and that we should invest the amount elsewhere. Would like to know your opinion.
Thanks,
Anju
You can surely pay a big chunk . Its just a start and will help you .. make it
You need to give application to wave off penalty for pre-payment in case of LICHFL else they may charge for this prepayment .
There is another condition which LICHFL has ,you can’t do pre-payment for first 6 months .Pls cross verify with LICHFL before paying .Clear all penalty clauses related doubts .
Dear Manish,
You need to be thanked for the work you are doing , I regularly read your comments and the way you answer all the queries is commendable . now coming to my query , i had taken a home loan for Rs 30 lacs ( under construction flat , payment goes based on amt disbursed) at 10.25% interest rate for 20 years from x bank , now i am transferring this loan to Y bank at 10.1% interest rate and was also thinking of reducing the tenure from 20 years to 10 /12 years , what do u suggest . thanks
Varun
First thing you can do is approach the existing bank and ask for the interest rate change if they allow . For change of tenure, the only option is to increase the EMI amount, you can do that if you can afford that !
Hi,
I have taken loan of 19,30,000 at 10.5 % variable rate of interest for the period of 20 years. The first part disbursement of the loan was for amount 13,00,000 (13 Lacs) done in Dec 2012. After two month of disbursement (i.e. in Feb) the rate of interest was reduced to 10.25%, and again in Sep 2013 it was increased to 11.00%. I had signed an agreement for reduced rate of interest at 10.25% from Dec 2013. The remaining amount of the loan (i.e. 6,30,000) will be disburse in Feb 2014. Kindly let me know, how to calculate the tenure after full disbursement and also if the rate of interest changes later on.
Shyam
Why do you want to calculate it, you can get the revised tenure info from your bank itself !
Manish,
Thanks for the detailed explaination on home loan. I don’t have home loan but in future this information is going to help me a lot. Thanks a lot!!
Good to hear that, you are slowing building your personal finance muscles 🙂
Hi Manish,
I have taken a home loan from ICICI bank “EMI Under Construction”, So far I have got two disbursements and two more disbursements are pending. When I got the sanction letter of home loan the interest rate was “10.5”, I had to pay EMI say “x” for 20 years. So far I have paid EMI for 9 months. Now, the interest rate has been increased to “10.75” and I was informed that still I have to pay EMI for 20 years and 4 months. I understood that “EMI under construction” doesn’t increase the EMI amount instead the tenure. But I am shocked that 0.25 increase in interest rate costs me so much i.e. increase in tenure means obviously I have to pay 12 months EMI extra?
Could you please throw some lights on this?
I am really confused about this loan and its traps
Thanks,
Deena
Deena
They are NOT Wrong . A small increase in interest rate can push your tenure by a big margin. You can calculate this yourself, In the EMI calculator, change interest rate number and see what tenure satisfied the same EMI amount.
But this should happen in start only , not at the end leg of the loan . Welcome to the world of Home loans !
Deena,
If you have some money to pay as re-payment ,pls pay ,it will reduce your tenure a lot .Suppose if you do prepayment of Rs.100000 ,it will reduce your tenure a lot .As said by Manish ,in starting year it makes lots of diff .Inquiry with your bank and if you have low interest generating saving use them for pre payment.
Hi Manish,
I have two queries,
1) In my Provisional certificate the intrest expected amount written as 59000/- per anum, However in final Intrest certificate the actual amount written as 83000/- per anum, How the calculation is been done? and To whom i concern about this(The Branch or Home loan department)
2) My Rate of Intrest gets down from 10.75 to 10.50 and 10.50 to 10.25 but no change in EMI. how do bank is working on this calculations….. would they decrese my loan tenure or intermediate amount adjustable?
Loan from Bank of India.
Please guide me on same.
Regards,
Rohit Prajapati
Hi Rohit
As its a PSU bank , I strongly suggest file a RTI and get answers from that, that will be the fastest way .
Hi Manish, your blog is very useful.
I have my home loan in SBI with 10.25% for 20 years for loan amount of Rs. 17,60000/-
I did the calculation as per the formula given in your blog.
It says my loan amount should be 17296/-, but i am paying 17580/-
Am I missing anything in the calculations?
May be the processing fees and other charges . Take the explaination from bank !
I had availed 1500000 housing loan from SBI in may 2015. I ve got last intalment of my loan on march 2016. Now i ve to repay my EMI from may 2016. My bank says it will be around 18000 pm for 14 years but my EMI calculator says it is around 16000pm plz solve my problem and calculate my EMI pm for sbi housing loan of 1500000 for 14 year
Thanks
Hi Pawan
This is very specific query which you should follow up with the concerned authority only. We wont be able to comment on that
Manish
Say i have taken a home loan with following details:
loan amount: 3000000 (thirty lakh)
interest:11%
tenure:25yrs(300 months)
Now my question is if i don’t pay any emi and I say that I will pay full amount after 300 months. What would be the amount I have to pay after 300 months
It will run into several crores . This is not how loan works 🙂 .
hello sir,
im plannin to construct a home, hence forth im applyin loan for 15lakh, where in interest rate is 10%.. hw 2 calculate emi?? usin ur formula, im endin up in an unknown number.. can u plz explain me.. thank u in advance
What is the number you are getting ?
sir for the loan amt of 1500000/- fifteen lakhs for 20 years, sir give in detail what the EMI Would be
+principle amt monthly
Check this – http://jagoinvestor.dev.diginnovators.site/calculators/html/loan-amortization.html
Dear shri Chouhan,
I shall be highly obilized if you please send me per year interest and principal for a housing loan of rs 2000000 for a240 months tenure @ 9.95% intt
Thanking you
s.k.khanna
You can do it using the sheet which are given at the end of the article http://jagoinvestor.dev.diginnovators.site/2011/04/loan-amortization-emi.html
hello sir I ‘ve taken a loan of Rs. 23,00,000 @10.75 for 20 years period. please calculate EMI rate as per above loan amt, interest and period.
You can do it here http://jagoinvestor.dev.diginnovators.site/calculators/html/EMI-Calculator.html